Use PY in Calculus¶
What is Function¶
我們可以將函數(functions)看作一台機器,當我們向這台機器輸入「x」時,它將輸出「f(x)」
這台機器所能接受的所有輸入的集合被稱為定義域(domian),其所有可能的輸出的集合被稱為值域(range)。函數的定義域和值域都十分重要,當我們知道一個函數的定義域,就不會將不合適的x扔給這個函數;知道了定義域就可以判斷一個值是否可能是這個函數所輸出的。
多項式(polynomials):¶
$f(x) = x^3 - 5^2 +9$ 因為這是個三次函數,當 $x\rightarrow \infty$ 時,$f(x) \rightarrow -\infty$,當 $x\rightarrow \infty$ 時,$f(x) \rightarrow \infty$ 因此,這個函數的定義域和值域都屬於實數集$R$。
def f(x):
return x**3 - 5*x**2 + 9
print(f(1), f(2))
通常,我們會繪製函數圖像來幫助我們來理解函數的變化
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-10,10,num = 1000)
y = f(x)
plt.plot(x,y)
指數函數(Exponential Functions)¶
$exp(x) = e^x$ domain is $(-\infty,\infty)$,range is $(0,\infty)$。在 py 中,我們可以利用歐拉常數 $e$ 定義指數函數:
def exp(x):
return np.e**x
print("exp(2) = e^2 = ",exp(2))
或者可以使用 numpy 自帶的指數函數:np.e**x
def eexp(x):
return np.e**(x)
print("exp(2) = e^2 = ",eexp(2))
plt.plot(x,exp(x))
當然,數學課就會講的更加深入$e^x$的定義式應該長成這樣:$\begin{align*}\sum_{k=0}^{\infty}\frac{x^k}{k!}\end{align*}$ 至於為什麼他會長成這樣,會在後面提及。
這個式子應該怎麼在python中實現呢?
def eeexp(x):
sum = 0
for k in range(100):
sum += float(x**k)/np.math.factorial(k)
return sum
print("exp(2) = e^2 = ",eeexp(2))
對數函數(Logarithmic Function)¶
$log_e(x) = ln(x)$
高中教的 $ln(x)$ 在大學和以後的生活中經常會被寫成 $log(x)$
對數函數其實就是指數函數的反函數,即,定義域為$(0,\infty)$,值域為$(-\infty,\infty)$。
numpy 為我們提供了以$2,e,10$ 為底數的對數函數:
x = np.linspace(1,10,1000,endpoint = False)
y1 = np.log2(x)
y2 = np.log(x)
y3 = np.log10(x)
plt.plot(x,y1,'red',x,y2,'yellow',x,y3,'blue')
三角函數(Trigonometric functions)¶
三角函數是常見的關於角的函數,三角函數在研究三角形和園等集合形狀的性質時,有很重要的作用,也是研究週期性現象的基礎工具;常見的三角函數有:正弦(sin),餘弦(cos)和正切(tan),當然,以後還會用到如餘切,正割,餘割等。
x = np.linspace(-10, 10, 10000)
a = np.sin(x)
b = np.cos(x)
c = np.tan(x)
# d = np.log(x)
plt.figure(figsize=(8,4))
plt.plot(x,a,label='$sin(x)$',color='green',linewidth=0.5)
plt.plot(x,b,label='$cos(x)$',color='red',linewidth=0.5)
plt.plot(x,c,label='$tan(x)$',color='blue',linewidth=0.5)
# plt.plot(x,d,label='$log(x)$',color='grey',linewidth=0.5)
plt.xlabel('Time(s)')
plt.ylabel('Volt')
plt.title('PyPlot')
plt.xlim(0,10)
plt.ylim(-5,5)
plt.legend()
plt.show()
複合函數(composition)¶
函數 $f$ 和 $g$ 複合,$f \circ g = f(g(x))$,可以理解為先把$x$ 輸入給 $g$ 函數,獲得 $g(x)$ 後在輸入函數 $f$ 中,最後得出:$f(g(x))$
- 幾個函數符合後仍然為一個函數
- 任何函數都可以看成若干個函數的複合形式
- $f\circ g(x)$ 的定義域與 $g(x)$ 相同,但是值域不一定與 $f(x)$ 相同
例:$f(x) = x^2, g(x) = x^2 + x, h(x) = x^4 +2x^2\cdot x + x^2$
def f(x):
return x**2
def g(x):
return x**2+x
def h(x):
return f(g(x))
print("f(1) equals",f(1),"g(1) equals",g(1),"h(1) equals",h(1))
x = np.array(range(-10,10))
y = np.array([h(i) for i in x])
plt.scatter(x,y,)
逆函數(Inverse Function)¶
給定一個函數$f$,其逆函數 $f^{-1}$ 是一個與 $f$ 進行複合後 $f\circ f^{-1}(x) = x$ 的特殊函數 函數與其反函數圖像一定是關於 $y = x$ 對稱的
def w(x):
return x**2
def inv(x):
return np.sqrt(x)
x = np.linspace(0,2,100)
plt.plot(x,w(x),'r',x,inv(x),'b',x,x,'g-.')
高階函數(Higher Order Function)¶
我们可以不局限于将数值作为函数的输入和输出,函数本身也可以作为输入和输出,
在給出例子之前,插一段話:
這裡介紹一下在 python中十分重要的一個表達式:lambda,lambda本身就是一行函數,他們在其他語言中被稱為匿名函數,如果你不想在程序中對一個函數使用兩次,你也許會想到用 lambda 表達式,他們和普通函數完全一樣。
原型:
lambda 參數:操作(參數)
add = lambda x,y: x+y
print(add(3,5))
這裡,我們給出 高階函數 的例子:
def horizontal_shift(f,H):
return lambda x: f(x-H)
上面定義的函數 horizontal_shift(f,H)。接受的輸入是一個函數 $f$ 和一個實數 $H$,然後輸出一個新的函數,新函數是將 $f$ 沿著水平方向平移了距離 $H$ 以後得到的。
x = np.linspace(-10,10,1000)
shifted_g = horizontal_shift(g,2)
plt.plot(x,g(x),'b',x,shifted_g(x),'r')
以高階函數的觀點去看,函數的複合就等於將兩個函數作為輸入給複合函數,然後由其產生一個新的函數作為輸出。所以複合函數又有了新的定義:
def composite(f,g):
return lambda x: f(g(x))
h3 = composite(f,g)
print (sum (h(x) == h3(x)) == len(x))
歐拉公式(Euler's Formula)¶
在前面給出了指數函數的多項式形式:$e^x = 1 + \frac{x}{1!} + \frac{x^2}{2!} + \dots = \sum_{k = 0}^{\infty}\frac{x^k}{k!}$ 接下來,我們不僅不去解釋上面的式子是怎麼來的,而且還要喪心病狂地扔給讀者:
三角函數:
$\begin{align*} &sin(x) = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}\dots = \sum_{k=0}^{\infty}(-1)^k\frac{x^{(2k+1)}}{(2k+1)!} \\ &cos(x) = \frac{x^0}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots =\sum_{k=0}^{\infty}(-1)^k\frac{x^{2k}}{2k!}\end{align*}$
在中學,我們曾經學過虛數 i (Imaginary Number)的概念,這裡我們對其來源和意義暫不討論,只是簡單回顧一下其基本的運算規則:
$i^0 = 1, i^1 = i, i^2 = -1 \dots$
將 $ix$ 帶入指數函數的公式中,得:
$\begin{align*}e^{ix} &= \frac{(ix)^0}{0!} + \frac{(ix)^1}{1!} + \frac{(ix)^2}{2!} + \dots \\ &= \frac{i^0 x^0}{0!} + \frac{i^1 x^1}{1!} + \frac{i^2 x^2}{2!} + \dots \\ &= 1\frac{x^0}{0!} + i\frac{x^i}{1!} -1\frac{x^2}{2!} -i\frac{x^3}{3!} \dots \\ &=(\frac{x^0}{0!}-\frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \dots ) + i(\frac{x^1}{1!} -\frac{x^3}{3!} + \frac{x^5}{5!}-\frac{x^7}{7!} + \dots \\&cos(x) + isin(x)\end{align*}$
此時,我們便可以獲得著名的歐拉公式:$e^{ix} = cos(x) + isin(x)$
令,$x = \pi$時,$\Rightarrow e^{i\pi} + 1 = 0$
歐拉公式在三角函數、圓周率、虛數以及自然指數之間建立的橋樑,在很多領域都扮演著重要的角色。
如果你對偶啦公式的正確性感到疑惑,不妨在Python中驗證一下:
import math
import numpy as np
a = np.sin(x)
b = np.cos(x)
x = np.pi
# the imaginary number in Numpy is 'j';
lhs = math.e**(1j*x)
rhs = b + (0+1j)*a
if(lhs == rhs):
print(bool(1))
else:
print(bool(0))
這裡給大家介紹一個很好的 Python 庫:sympy,如名所示,它是符號數學的 Python 庫,它的目標是稱為一個全功能的計算機代數系統,同時保證代碼簡潔、易於理解和拓展;
所以,我們也可以通過 sympy 來展開 $e^x$ 來看看它的結果是什麼🙂
import sympy
z =sympy.Symbol('z',real = True)
sympy.expand(sympy.E**(sympy.I*z),complex = True)
將函數寫成多項式形式有很多的好處,多項式的微分和積分都相對容易。這是就很容易證明這個公式了:
$\frac{d}{dx}e^x = e^x \frac{d}{dx}sin(x) = cos(x)\frac{d}{dx}cos(x) = -sin(x)$
喔,對了,這一章怎麼能沒有圖呢?收尾之前來一發吧: 我也不知道这是啥 🤨
import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d
x,y=np.mgrid[-2:2:20j,-2:2:20j]
z=x*np.exp(-x**2-y**2)
ax=plt.subplot(111,projection='3d')
ax.plot_surface(x,y,z,rstride=2,cstride=1,cmap=plt.cm.coolwarm,alpha=0.8)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.show()
泰勒級數¶
泰勒級數(Taylor Series)¶
在前幾章的預熱之後,讀者可能有這樣的疑問,是否任何函數都可以寫成友善的多項式形式呢? 到目前為止,我們介紹的$e^x$, $sin(x)$, $cos(x)$ 都可以用多項式進行表達。其實,這些多項式實際上就是這些函數在 $x=0$ 處展開的泰勒級數。
下面我們給出函數 $f(x)$ 在$x=0$ 處展開的泰勒級數的定義:
$\begin{align*}f(x) = f(0) + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3 + \dots = \sum^{\infty}{k = 0} \frac{f^{(k)}(0)}{k!}x^k \end{align*}$
其中:$f^{(k)}(0)$ 表示函數 $f$ 在 $k$ 次導函數在 $x=0$ 的取值。
我們知道 $e^x$ 無論計算多少次導數結果出來都是 $e^x$
即,$exp(x) = exp'(x)=exp''(x)=exp'''(x)=exp'''(x) = \dots$
因而,根據上面的定義展開:
$\begin{align*}exp(x) &= exp(0) + \frac{exp'(0)}{1!}+\frac{exp''(0)}{2!}x^2 +\frac{exp'''(0)}{3!}x^3 + \dots \\ &=1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots \\&=\sum_{k=0}^{\infty}\frac{x^k}{k!}\end{align*}$
多項式近似(Polynomial Approximation)¶
泰勒級數,可以把非常複雜的函數變成無限項的和的形式。通常,我們可以只計算泰勒級數的前幾項和,就可以獲得原函數的局部近似了。在做這樣的多項式近似時,我們所計算的項越多,則近似的結果越精確。
下面,開始使用 python 做演示
import sympy as sy
import numpy as np
from sympy.functions import sin,cos
import matplotlib.pyplot as plt
plt.style.use("ggplot")
# Define the variable and the function to approximate
x = sy.Symbol('x')
f = sin(x)
# Factorial function
def factorial(n):
if n <= 0:
return 1
else:
return n*factorial(n-1)
# Taylor approximation at x0 of the function 'function'
def taylor(function,x0,n):
i = 0
p = 0
while i <= n:
p = p + (function.diff(x,i).subs(x,x0))/(factorial(i))*(x-x0)**i
i += 1
return p
# Plot results
def plot():
x_lims = [-5,5]
x1 = np.linspace(x_lims[0],x_lims[1],800)
y1 = []
# Approximate up until 10 starting from 1 and using steps of 2
for j in range(1,10,2):
func = taylor(f,0,j)
print('Taylor expansion at n='+str(j),func)
for k in x1:
y1.append(func.subs(x,k))
plt.plot(x1,y1,label='order '+str(j))
y1 = []
# Plot the function to approximate (sine, in this case)
plt.plot(x1,np.sin(x1),label='sin of x')
plt.xlim(x_lims)
plt.ylim([-5,5])
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.title('Taylor series approximation')
plt.show()
plot()
展開點(Expansion Point)¶
上述的式子,都是在 $x=0$ 進行的,我們會發現多項式近似只在 $x=0$ 處較為準確。但,這不代表,我們可以在別的點進行多項式近似,如$x=a$ : $f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \dots $
import sympy
x = sympy.Symbol('x',real = True)
f = lambda x: x**x-2*x-6
y = f(x)
print(y.limit(x,2))
函數的連續性¶
極限可以用來判斷一個函數是否為連續函數。 當極限$\begin{align*}\lim_{x\rightarrow a} f(x)= f(a)\end{align*}$時,稱函數$f(x)$在點$ x = a$ 處為連續的。當一個函數在其定義域中任意一點均為連續,則稱該函數是連續函數。
泰勒級數用於極限計算¶
我們在中學的時候,學習過關於部分極限的計算,這裡不再贅述。泰勒級數也可以用於計算一些形式比較複雜的函數的極限。這裡,僅舉一個例子:
$\begin{align*} \lim_{x\rightarrow 0}\frac{sin(X)}{x} &= lim_{x\rightarrow 0} \frac{\frac{x}{1!}-\frac{x^3}{3!}\dots }{x} \\ &= \lim_{x\rightarrow 0} \frac{x(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots}{x} \\ &= \lim_{x\rightarrow 0} 1 -\frac{x^2}{3!} + \frac{x^4}{5!}-\frac{x^6}{7!}+\dots \\& = 1 \end{align*}$
洛必達法則(l'Hopital's rule)¶
在高中,老師就教過的一個神奇的法則:如果我們在求極限的時候,所求極限是無窮的,那我們可以試一下使用洛必達法則,哪些形式呢:$\frac{0}{0}, \frac{\infty}{\infty}, \frac{\infty}{0}$等等。這裡,我們要注意一個前提條件:上下兩個函數都是連續函數才可以使用洛必達法則這裡我們用 $\frac{0}{0}$ 作為一個例子:
$\begin{align*}\lim_{x \rightarrow a}\frac{f'(x)}{g'(x)} \\
= \lim_{x \rightarrow a}\frac{f'(x)}{g'(x)} \end{align*}$
若此時,分子分母還都是$0$的話,再次重複:$\begin{align*}\lim_{x \rightarrow a}\frac{f''(x)}{g''(x)}\end{align*}$
大$O$記法(Big-O Notation)¶
這個我在網上能找到的資料很少,大多是算法的時間複雜度相關的資料
算法複雜度的定義:
We denote an algorithm has a complexity of O(g(n))if there exists a constants $c \in R^+$, suchthat $t(n)\leq c\cdot g(n), \forall n\geq 0$.
這裡的$n$是算法的輸入大小(input size),可以看作變量的個數等等。
方程$t$在這裡指算法的“時間”,也可以看作執行基本算法需要的步驟等等。
方程$g$在這裡值得是任意函數。
我們也可以將這個概念用在函數上:
我們已經見過了很多函數,在比較這兩個函數時,我們可能會知道,隨著輸入值$x$的增加或者減少,兩個函數的輸出值,兩個函數的輸出值增長或者減少的速度究竟是誰快誰慢,哪一個函數最終會遠遠甩開另一個。
通過繪製函數圖像,我們可以得到一些之直觀的感受:
import numpy as np
import matplotlib.pyplot as plt
m= range(1,7)
fac = [np.math.factorial(i) for i in m] #fac means factorial#
exponential = [np.e**i for i in m]
polynomial = [i**3 for i in m]
logarithimic = [np.log(i) for i in m]
plt.plot(m,fac,'black',m,exponential,'blue',m,polynomial,'green',m,logarithimic,'red')
plt.show()
根據上面的圖,我們可以看出$x \rightarrow \infty$ 時,$x! > e^x > x^3 > ln(x)$ ,想要證明的話,我們需要去極限去算(用洛必達法則)。
$\begin{align*}\lim_{x\rightarrow \infty}\frac{e^x}{x^3} = \infty \end{align*}$ 可以看出,趨於無窮時,分子遠大於分母,反之同理。
我們可以用 sympy 來算一下這個例子:
import sympy
import numpy as np
x = sympy.Symbol('x',real = True)
f = lambda x: np.e**x/x**3
y = f(x)
print(y.limit(x,oo))
為了描述這種隨著輸入$x\rightarrow \infty$或$x \rightarrow 0$時,函數的表現,我們如下定義大$O$記法:
若我們稱函數$f(x)$在$x\rightarrow 0$時,時$O(g(x))$,則需要找到一個常數$C$,對於所有足夠小的$x$均有$|f(x)|<C|g(x)|$
若我們稱函數$f(x)$在$x\rightarrow 0$時是$O(g(x))$,則需要找一個常數$C$,對於所有足夠大的$x$均有$|f(x)|<C|g(x)|$
大$O$記法之所以得此名稱,是因為函數的增長速率很多時候被稱為函數的階(Order)
下面舉一個例子:當$x\rightarrow \infty$時,$x\sqrt{1+x^2}$是$O(x^2)$
import sympy
import numpy as np
import matplotlib.pyplot as plt
x = sympy.Symbol('x',real = True)
xvals = np.linspace(0,100,1000)
f = x*sympy.sqrt(1+x**2)
g = 2*x**2
y1 = [f.evalf(subs = {x:xval}) for xval in xvals]
y2 = [g.evalf(subs = {x:xval}) for xval in xvals]
plt.plot(xvals[:10],y1[:10],'r',xvals[:10],y2[:10],'b')
plt.show()
plt.plot(xvals,y1,'r',xvals,y2,'b')
plt.show()
import numpy as np
from sympy.abc import x
import matplotlib.pyplot as plt
# function
f = x**3-3*x-6
# the tengent line at x=6
line = 106*x-428
d4 = np.linspace(5.9,6.1,100)
domains = [d3]
# define the plot funtion
def makeplot(f,l,d):
plt.plot(d,[f.evalf(subs={x:xval}) for xval in d],'b',\
d,[l.evalf(subs={x:xval}) for xval in d],'r')
for i in range(len(domains)):
# draw the plot and the subplot
plt.subplot(2, 2, i+1)
makeplot(f,line,domains[i])
plt.show()
切線(Tangent Line)¶
中學介紹導數的時候,通常會舉兩個例子,其中一個是幾何意義上的例子:對於函數關於某一點進行球道,得到的是函數在該點處切線的斜率。 選中函數圖像中的某一點,然後不斷地將函數圖放大,當我們將鏡頭拉至足夠近後便會發現函數圖看起來像一條直線,這條直線就是切線。
import numpy as np
from sympy.abc import x
import matplotlib.pyplot as plt
# function
f = x**3-2*x-6
# the tengent line at x=6
line = 106*x-438
d1 = np.linspace(2,10,1000)
d2 = np.linspace(4,8,1000)
d3 = np.linspace(5,7,1000)
d4 = np.linspace(5.9,6.1,100)
domains = [d1,d2,d3,d4]
# define the plot funtion
def makeplot(f,l,d):
plt.plot(d,[f.evalf(subs={x:xval}) for xval in d],'b',\
d,[l.evalf(subs={x:xval}) for xval in d],'r')
for i in range(len(domains)):
# draw the plot and the subplot
plt.subplot(2, 2, i+1)
makeplot(f,line,domains[i])
plt.show()
另一個例子就是:對路程的時間函數 $s(t)$ 求導可以得到速度的時間函數 $v(t)$,再進一步求導可以得到加速度的時間函數 $a(t)$。這個比較好理解,因為函數真正關心的是:當我們稍稍改變一點函數的輸入值時,函數的輸出值有怎樣的變化。
導數(Derivative)¶
導數的定義如下:
定義一:
$\begin{align*}f'(a) = \frac{df}{dx}\mid_{x=a} = \lim_{x\rightarrow 0} \frac{f(x)-f(a)}{x-a}\end{align*}$
若該極限不存在,則函數在 $x=a$ 處的導數也不存在。
定義二:
$\begin{align*}f'(a) = \frac{df}{dx}\mid_{x=a} = \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h}\end{align*}$
以上两个定义都是耳熟能详的定义了,这里不多加赘述。
定義三:
函數$f(x)$在$x=a$處的導數$f'(a)$是滿足如下條件的常數$C$:
對於在$a$附近輸入值的微笑變化$h$有,$f(a+h)=f(a) + Ch + O(h^2)$ 始終成立,也就是說導數$C$是輸出值變化中一階項的係數。
$\begin{align*} \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} = \lim_{h\rightarrow 0} C + O(h) = C \end{align*}$
下面具一個例子,求$cos(x)$在$x=a$處的導數:
$\begin{align*} cos(a+h) &= cos(a)cos(h) - sin(a)sin(h)\\&=cos(a)(a+O(h^2)) - sin(a)(h+O(h^3))\\&=cos(a)-sin(a)h+O(h^2)\end{align*}$
因此,$\frac{d}{dx}cos(x)\mid_{x=a} = -sin(a)$
import numpy as np
from sympy.abc import x
f = lambda x: x**3-2*x-6
def derivative(f,h=0.00001):#define the 'derivative' function
return lambda x: float(f(x+h)-f(x))/h
fprime = derivative(f)
print (fprime(6))
#use sympy's defult derivative function
from sympy.abc import x
f = x**3-2*x-6
print(f.diff())
print(f.diff().evalf(subs={x:6}))
線性近似(Linear approximation)¶
定義:就是用線性函數去對普通函數進行近似。依據導數的定義三,我們有:$f(a+h) = f(a) + f'(a)h + O(h^2)$ 如果,我們將高階項去掉,就獲得了$f(a+h)$的線性近似式了:$f(a+h) = \approx f(a) + f'(a)h$
舉個例子,用線性逼近去估算:
$\begin{align*} \sqrt{255} &= \sqrt {256-1} \approx \sqrt{256} + \frac{1}{2\sqrt{256}(-1)} \\ &=16-\frac{1}{32} \\ &=15 \frac{31}{32} \end{align*}$
牛頓迭代法(Newton's Method)¶
它是一種用於在實數域和複數域上近似求解方程的方法:使用函數$f(x)$的泰勒級數的前面幾項來尋找$f(X)=0$的根。
首先,選擇一個接近函數$f(x)$零點的$x_0$,計算對應的函數值$f(x_0)$和切線的斜率$f'(x_0)$;
然後計算切線和$x$軸的交點$x_1$的$x$座標:$ 0 = (x_1 - x_0)\cdot f'(x_0) + f(x_0)$;
通常來說,$x_1$ 會比 $x_0$ 更接近方程$f(X)=0$的解。因此, 我們現在會利用$x_1$去開始新一輪的迭代。公式如下:
$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$
from sympy.abc import x
def mysqrt(c, x = 1, maxiter = 10, prt_step = False):
for i in range(maxiter):
x = 0.5*(x+ c/x)
if prt_step == True:
# 在输出时,{0}和{1}将被i+1和x所替代
print ("After {0} iteration, the root value is updated to {1}".format(i+1,x))
return x
print (mysqrt(2,maxiter =4,prt_step = True))
我們可以通過畫圖,更加了解牛頓法
import numpy as np
import matplotlib.pyplot as plt
f = lambda x: x**2-2*x-4
l1 = lambda x: 2*x-8
l2 = lambda x: 6*x-20
x = np.linspace(0,5,100)
plt.plot(x,f(x),'black')
plt.plot(x[30:80],l1(x[30:80]),'blue', linestyle = '--')
plt.plot(x[66:],l2(x[66:]),'blue', linestyle = '--')
l = plt.axhline(y=0,xmin=0,xmax=1,color = 'black')
l = plt.axvline(x=2,ymin=2.0/18,ymax=6.0/18, linestyle = '--')
l = plt.axvline(x=4,ymin=6.0/18,ymax=10.0/18, linestyle = '--')
plt.text(1.9,0.5,r"$x_0$", fontsize = 18)
plt.text(3.9,-1.5,r"$x_1$", fontsize = 18)
plt.text(3.1,1.3,r"$x_2$", fontsize = 18)
plt.plot(2,0,marker = 'o', color = 'r' )
plt.plot(2,-4,marker = 'o', color = 'r' )
plt.plot(4,0,marker = 'o', color = 'r' )
plt.plot(4,4,marker = 'o', color = 'r' )
plt.plot(10.0/3,0,marker = 'o', color = 'r' )
plt.show()
下面舉一個例子,$f(x) = x^2 -2x -4 = 0$的解,從$x_0 = 4$ 的初始猜測值開始,找到$x_0$的切線:$y=2x-8$,找到與$x$軸的交點$(4,0)$,將此點更新為新解:$x_1 = 4$,如此循環。
def NewTon(f, s = 1, maxiter = 100, prt_step = False):
for i in range(maxiter):
# 相较于f.evalf(subs={x:s}),subs()是更好的将值带入并计算的方法。
s = s - f.subs(x,s)/f.diff().subs(x,s)
if prt_step == True:
print("After {0} iteration, the solution is updated to {1}".format(i+1,s))
return s
from sympy.abc import x
f = x**2-2*x-4
print(NewTon(f, s = 2, maxiter = 4, prt_step = True))
另外,我們可以使用sympy,它可以幫助我們運算
import sympy
from sympy.abc import x
f = x**2-2*x-4
print(sympy.solve(f,x))
from sympy.abc import x
from sympy.abc import y
import matplotlib.pyplot as plt
f = x**2*y-2*x*y
print(f.diff(x,2)) #the second derivatives of x
print(f.diff(x).diff(x))# the different writing of the second derivatives of x
print(f.diff(x,y)) # we first get the derivative of x , then get the derivative of y
优化问题(Optimization Problem)¶
在微積分中,優化問題常常指的是算最大面積,最大體積等,現在給出一個例子:
plt.figure(1, figsize=(4,4))
plt.axis('off')
plt.axhspan(0,1,0.2,0.8,ec="none")
plt.axhspan(0.2,0.8,0,0.2,ec="none")
plt.axhspan(0.2,0.8,0.8,1,ec="none")
plt.axhline(0.2,0.2,0.8,linewidth = 2, color = 'black')
plt.axhline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axhline(1,0.17,0.23,linewidth = 2, color = 'black')
plt.axvline(0.2,0.8,1,linewidth = 2, color = 'black')
plt.axhline(0.8,0.17,0.23,linewidth = 2, color = 'black')
plt.axhline(1,0.17,0.23,linewidth = 2, color = 'black')
plt.text(0.495,0.22,r"$l$",fontsize = 18,color = "black")
plt.text(0.1,0.9,r"$\frac{4-1}{2}$",fontsize = 18,color = "black")
plt.show()
用一張給定邊長$4$的正方形紙來一個沒有蓋的紙盒,設這個紙盒的底部邊長為$l$,紙盒的高為$\frac{4-l}{2}$,那麼紙盒的體積為:
$V(l) = l^2\frac{4-l}{2}$
我們會希望之道,怎麼樣得到$ max\{V_1, V_2, \dots V_n\}$ ;優化問題就是在滿足條件下,使得目標函數(objective function)得到最大值(或最小)。
import numpy as np
import matplotlib.pyplot as plt
l = np.linspace(0,4,100)
V = lambda l: 0.5*l**2*(4-l) # the 'l' is the charcter 'l', not the number'one' as '1'
plt.plot(l,V(l))
plt.vlines(2.7,0,5, colors = "c", linestyles = "dashed")
plt.show()
通過觀察可得,在$l$的值略大於$2.5$的位置(虛線),獲得最大體積。
關鍵點(Critical Points)¶
通過導數一節,我們知道一個函數在某一處的導數是代表了在輸入後函數值所發生的相對應的變化。
因此,如果在給定一個函數$f$,如果知道點$x=a$處函數的導數不為$0$,則在該點處稍微改變函數的輸入值,函數值會發生變化,這表明函數在該點的函數值,既不是局部最大值(local maximum),也不是局部最小值(local minimum);相反,如果函數$f$在點$x=a$處函數的導數為$0$,或者該點出的導數不存在則稱這個點為關鍵點(critical Plints)
要想知道一個$f'(a)=0$的關鍵處,函數值$f(a)$是一個局部最大值還是局部最小值,可以使用二次導數測試:
- 如果 $f''(a) > 0$, 則函數$f$在$a$處的函數值是局部最小值;
- 如果 $f''(a) < 0$, 則函數$f$在$a$處的函數值是局部最大值;
- 如果 $f''(a) = 0$, 則無結論。
二次函數測試在中學課本中,大多是要求不求甚解地記憶的規則,其實理解起來非常容易。二次導數測試中涉及到函數在某一點處的函數值、一次導數和二次導數,於是我們可以利用泰勒級數:$f(x)$在$x=a$的泰勒級數:
$f(x) = f(a) + f'(a)(x-a) + \frac{1}{2}f''(a)(x-a)^2 + \dots$
因為$a$是關鍵點,$f'(a)$ = 0, 因而:$f(x) = f(a) + \frac{1}{2}f''(a)(x-a)^2 + O(x^3)$ 表明$f''(a) \neq 0$時,函數$f(x)$在$x=a$附近的表現近似於二次函數,二次項的係數$\frac{1}{2}f''(a)$決定了函數值在該點的表現。
回到剛才那題:求最大體積,現在,我們就可以求了:
import sympy
from sympy.abc import l
V = 0.5*l**2*(4-l)
# first derivative
print(V.diff(l))
# the domain of first derivative is (-oo,oo),so, the critical point is the root of V'(1) = 0
cp = sympy.solve(V.diff(l),l)
print(str(cp))
#after finding out the critical point, we can calculate the second derivative
for p in cp:
print(int(V.diff(l,2).subs(l,p)))
# known that whenl=2.666..., we get the maximum V
線性迴歸(Linear Regression)¶
二維平面上有$n$個數據點,$p_i = (x_i,y_i)$,現在嘗試找到一條經過原點的直線$y=ax$,使得所有數據點到該直線的殘差(數據點和回歸直線之間的水平距離)的平方和最小。
import numpy as np
import matplotlib.pyplot as plt
# Set seed of random function to ensure reproducibility of simulation data
np.random.seed(123)
# Randomly generate some data with errors
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res
# Solve the coefficient of the regression line
a = sum(x*y)/sum(x**2)
# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red')
for i in range(len(x)):
plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\
max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\
color = 'black')
plt.show()
要找到這樣一條直線,實際上是一個優化問題:
$\min_a Err(a) = \sum_i(y_i - ax_i)^2$
要找出函數$Err(a)$的最小值,首先計算一次導函數:$\frac{dErr}{da} = \sum_i 2(y_i-ax_i)(-x_i)$,因此,$a = \frac{\sum_i x_iy_i}{\sum_i x_i^2}$ 是能夠使得函數值最小的輸入。
這也是上面python代碼中,求解回歸線斜率所用的計算方式。
如果,我們不限定直線一定經過原點,即,$y=ax+b$,則變量變成兩個:$a$和$b$:
$\min_a Err(a,b) = \sum_i(y_i - ax_i-b)^2$
這個問題就是多元微積分中所要分析的問題了,這裡給出一種python中的解法:
import numpy as np
import matplotlib.pyplot as plt
# 设定好随机函数种子,确保模拟数据的可重现性
np.random.seed(123)
# 随机生成一些带误差的数据
x = np.linspace(0,10,10)
res = np.random.randint(-5,5,10)
y = 3*x + res
# 求解回归线的系数
a = sum(x*y)/sum(x**2)
slope, intercept = np.polyfit(x,y,1)
# 绘图
plt.plot(x,y,'o')
plt.plot(x,a*x,'red',linestyle='--')
plt.plot(x,slope*x+intercept, 'blue')
for i in range(len(x)):
plt.axvline(x[i],min((a*x[i]+5)/35.0,(y[i]+5)/35.0),\
max((a*x[i]+5)/35.0,(y[i]+5)/35.0),linestyle = '--',\
color = 'black')
plt.show()
定積分(Integral)¶
也被稱為黎曼積分(Riemann integral),直觀地說,對於一個給定的正實數值函數$f(x)$,$f(x)$在一個實數區間$[a,b]$上的定積分:$\int_a^b f(x) dx$ 可以理解成在$O-xy$坐標平面上,由曲線$(x,f(x))$,直線$x=a, x=b$以及$x$軸圍成的面積。
x = np.linspace(0, 5, 100)
y = np.sqrt(x)
plt.plot(x, y)
plt.fill_between(x, y, interpolate=True, color='b', alpha=0.5)
plt.xlim(0,5)
plt.ylim(0,5)
plt.show()
黎曼積分的核心思想就是試圖通過無限逼近來確定這個積分值。同時請注意,如果$f(x)$取負值,則相應的面積值$S$也取負值。這裡不給出詳細的證明和分析。不太嚴格的講,黎曼積分就是當分割的月來月“精細”的時候,黎曼河去想的極限。下面的圖就是展示,如何通過“矩形逼近”來證明。(這裡不提及勒貝格積分 Lebesgue integral)
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
def func(x):
return -x**3 - x**2 + 5
a, b = 2, 9 # integral limits
x = np.linspace(-5, 5)
y = func(x)
ix = np.linspace(-5, 5,10)
iy = func(ix)
fig, ax = plt.subplots()
plt.plot(x, y, 'r', linewidth=2, zorder=5)
plt.bar(ix, iy, width=1.1, color='b', align='edge', ec='olive', ls='-', lw=2,zorder=5)
plt.figtext(0.9, 0.05, '$x$')
plt.figtext(0.1, 0.9, '$y$')
ax.spines['left'].set_visible(True)
ax.spines['right'].set_visible(True)
ax.xaxis.set_major_locator(ticker.IndexLocator(base=1, offset=0))
plt.xlim(-6,6)
plt.ylim(-100,100)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
def func(x):
return -x**3 - x**2 + 5
a, b = 2, 9 # integral limits
x = np.linspace(-5, 5)
y = func(x)
ix = np.linspace(-5, 5,20)
iy = func(ix)
fig, ax = plt.subplots()
plt.plot(x, y, 'r', linewidth=2, zorder=5)
plt.bar(ix, iy, width=1.1, color='b', align='edge',ec='olive', ls='-', lw=2,zorder=5)
plt.figtext(0.9, 0.05, '$x$')
plt.figtext(0.1, 0.9, '$y$')
ax.spines['left'].set_visible(True)
ax.spines['right'].set_visible(True)
ax.xaxis.set_major_locator(ticker.IndexLocator(base=1, offset=0))
plt.xlim(-6,6)
plt.ylim(-100,100)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
def func(x):
n = 10
return n / (n ** 2 + x ** 3)
a, b = 2, 9 # integral limits
x = np.linspace(0, 11)
y = func(x)
x2 = np.linspace(1, 12)
y2 = func(x2-1)
ix = np.linspace(1, 10, 10)
iy = func(ix)
fig, ax = plt.subplots()
plt.plot(x, y, 'r', linewidth=2, zorder=15)
plt.plot(x2, y2, 'g', linewidth=2, zorder=15)
plt.bar(ix, iy, width=1, color='r', align='edge', ec='olive', ls='--', lw=2,zorder=10)
plt.ylim(ymin=0)
plt.figtext(0.9, 0.05, '$x$')
plt.figtext(0.1, 0.9, '$y$')
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.xaxis.set_major_locator(ticker.IndexLocator(base=1, offset=1))
plt.show()
不定積分(indefinite integral)¶
如果,我們將求導看作一個高階函數,輸入進去的一個函數,求導後成為一個新的函數。那麼不定積分可以視作求導的「反函數」,$F'(x) = f(x)$ ,則$\int f(x)dx = F(x) + C$,
寫成類似於反函數之間的複合的形式有:$\int((\frac{d}{dx}F(x))dx) = F(x) + C, \ \ C \in R$
即,在微積分中,一個函數$f = f$的不定積分,也稱為原函數或反函數,是一個導數等於$ f=f $的函數$ f = F $,即,$f = F' = f$。不定積分和定積分之間的關係,由 微積分基本定理 確定。
$\int f(x) dx = F(x) + C$ 其中$f = F$ 是 $f = f$的不定積分。這樣,許多函數的定積分的計算就可以簡便的通過求不定積分來進行了。
這裡介紹python中的實現方法
print(a.integrate())
print(sympy.integrate(sympy.E**t+3*t**2))
常微分方程(Ordinary Differential Equations,ODE)¶
我們觀察一輛行駛的汽車,假設我們發現函數$a(t)$能夠很好地描述這輛汽車在各個時刻的加速度,因為對速度的時間函數(v-t)求導可以得到加速度的時間函數(a-t),如果我們希望根據$a(t)$求出$v(t)$,很自然就會得出下面的方程:
$\frac{dv}{dt}=a(t)$;如果我們能夠找到一個函數滿足:$\frac{dv}{dt} = a(t)$,那麼$v(t)$就是上面房車的其中一個解,因為常數項求導的結果是$0$,那麼$\forall C \in R$,$v(t)+C$也都是這個方程的解,因此,常微分方程的解就是$set \ = \{v(t) + C\}$
在得到這一系列的函數後,我們只需要知道任意一個時刻裡汽車行駛的速度,就可以解出常數項$C$,從而得到最終想要的一個速度時間函數。
如果我們沿用「導數是函數在某一個位置的切線斜率」這一種解讀去看上面的方正,就像是我們知道了一個函數在各個位置的切線斜率,反過來曲球這個函數一樣。
import sympy
t = sympy.Symbol('t')
c = sympy.Symbol('c')
domain = np.linspace(-3,3,100)
v = t**3-3*t-6
a = v.diff()
for p in np.linspace(-2,2,20):
slope = a.subs(t,p)
intercept = sympy.solve(slope*p+c-v.subs(t,p),c)[0]
lindomain = np.linspace(p-1,p+1,20)
plt.plot(lindomain,slope*lindomain+intercept,'red',linewidth = 1)
plt.plot(domain,[v.subs(t,i) for i in domain],linewidth = 2)
極坐標分割¶
同樣的,極座標也是按照自變量進行分割。這是由函數的影射關係決定的,一直自變量,通過函數運算,就可以得到函數值。從圖形上看,這樣分割可以是的每個分割單元“不規則的邊”的數量最小,最好是只有一條。所以,在實際問題建模時,重要的是選取合適的坐標系。
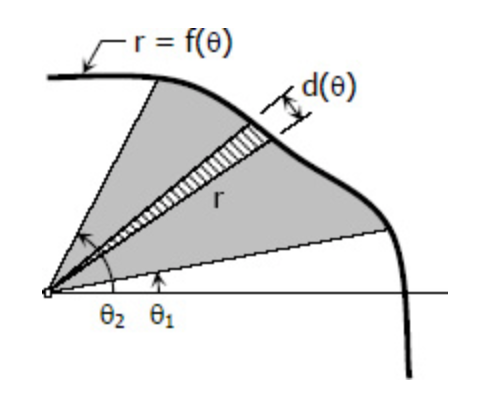
近似¶
近似,是微積分中重要的一部,通過近似將分割出來的不規則的“單元”近似成一個規則的”單元“。跟上面一樣,我們無法直接計算曲線圍成的面積,但是可以用一個相似的矩形去替代。
- Riemann 的定義的例子:在待求解的是區間$[a, b]$上曲線與$x$軸圍成的面積,因此套用的是平面的面積公式:$S_i = h_i \times w_i = f(\xi) \times \Delta x_i$
- 極坐標系曲線積分
待求解的是在區間$[\theta_1, \theta_2]$上曲線與原點圍成的面積,因此套用的圓弧面積公式:$S_i = \frac{1}{2}\times r_i^2 \times \Delta \theta_i = \frac{1}{2} \times [f(\xi_i)^2 \times \Delta \theta_i$ - 平面曲線長度
平面曲線在微觀上近似為一段“斜線”,那麼,它遵循的是“勾股定理”了,即“Pythagoras 定理”:$\Delta l_i = \sqrt{(\Delta x_i)^2 + (\Delta y_i)^2} = \sqrt{1 + (\frac{\Delta y_i}{\Delta x_i}^2 \Delta x_i}$ - 極坐標曲線長度
$dl = \sqrt{(dx)^2 + (dy)^2 } = \sqrt{ \frac{d^2[r(\theta)\times cos(\theta)]}{d\theta^2} + \frac{d^2[r(\theta)\times sin(\theta)]}{d\theta^2} d\theta } = \sqrt{ r^2(\theta) + r'^2(\theta)}d\theta$
我們不能直接用弧長公式,弧長公式的推導用了$\pi$,而$\pi$本身就是一個近似值
求和¶
前面幾步都是在微觀層面進行的,只有通過“求和”(Remann 和)才能回到宏觀層面:$\lim_{\lambda \rightarrow 0^+}\sum_{i = 0}^n F_i$ 其中,$F_i$ 表示各種圍觀單元的公式。
例題:求(lemniscate)$\rho^2 = 2a^2 cos(2\theta)$ 圍成的平民啊區域的面積。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
alpha = 1
theta = np.linspace(0, 2*np.pi, num=1000)
x = alpha * np.sqrt(2) * np.cos(theta) / (np.sin(theta)**2 + 1)
y = alpha * np.sqrt(2) * np.cos(theta) * np.sin(theta) / (np.sin(theta)**2 + 1)
plt.plot(x, y)
plt.grid()
plt.show()
這是一個對稱圖形,只需要計算其中的四分之一區域面積即可
from sympy import *
t, a = symbols('t a')
f = a ** 2 * cos(2 * t)
4 * integrate(f, (t, 0, pi / 4))